samedi 31 octobre 2015
Représentativité et significativité des analyses
Vous entendez régulièrement les termes d’échantillons représentatifs, de résultats significatifs. Toutefois, lors de l’analyse de vos résultats, ces concepts vous semblent abstraits. Nous proposons, dans ce billet, un rappel de ces deux notions statistiques pour vous permettre d’interpréter et utiliser vos résultats au mieux.
Représentativité de vos résultats
Il est rare qu’une enquête puisse être administrée sur l’ensemble des individus d’une population. Il faut donc au préalable constituer un échantillon à interroger [1].
Un échantillon est dit représentatif lorsqu’il possède les mêmes caractéristiques que la population mère, caractéristiques jugées discriminantes de la population. Ces caractéristiques dépendent du secteur sur lequel l’enquête est effectuée.
Une entreprise, proposant des prestations en BtoB, se focalisera sur le chiffre d’affaires et le secteur de ses clients, alors qu’une entreprise opérant sur un marché BtoC préférera travailler sur les caractéristiques de ses consommateurs (sexe, csp, tranche d’âge …).
Exemple

L’échantillon de répondants n’est pas représentatif de la population mère, qui compte 20% de « contact SAV ». Si l’on conserve la base de répondants sans opération statistique, les résultats des « Contact SAV » auront un poids plus important que dans la réalité. Les résultats seront directement impactés par les mauvais résultats SAV.
Niveau de satisfaction global sans redressement =39,4 %
Niveau de satisfaction global avec redressement = 52,6 %
Dans le cas des études auto-administrées, dont les retours dépendent de la « bonne volonté » des individus, tout travail d’analyse doit débuter par la vérification de la représentativité de l’échantillon obtenu. Si tel n’est pas le cas, il apparait alors nécessaire de redresser les résultats avant toute interprétation.
Significativité et Intervalle de Confiance (IC)
Lorsque vous travaillez sur un échantillon, vous obtenez une « estimation » des phénomènes existants au sein de la population mère. Ainsi, involontairement, vous acceptez de travailler avec une marge d’erreur, écart entre les niveaux de satisfaction de l’échantillon et les niveaux observés dans la réalité.
La marge d’erreur (ou encore Intervalle de confiance) se mesure à partir de :
- la taille de l’échantillon : plus l’échantillon est grand, plus la mesure est précise
- un seuil de significativité : niveau de confiance des résultats
Le seuil de significativité vous permet de définir le degré de certitude avec lequel vous obtenez vos résultats. Si vos chiffres sont déclarés significatifs à 95%, cela signifie que vos résultats sont à l’intérieur de l’intervalle de confiance avec 95% de certitude. Autrement dit il existe 5% de risque que vos résultats soient en dehors de l’intervalle de confiance calculé.
De manière générale, on utilise le seuil de significativité de 5% pour déclarer des résultats comme significatifs. Toutefois, dans le cadre d’estimation des comportements/perceptions humain(e)s, il ne faut pas complément ignorer les résultats pour lesquels le seuil de significativité est compris entre 5% et 10%.
Les règles de statistique communes, utilisées pour calculer le seuil de significativité, s’appliquent sur des grands échantillons. En dessous de 30 répondants, les paramètres ne sont plus exploitables selon les lois statistiques. C’est pourquoi Sharing-Data vous propose une annotation pour faciliter votre lecture des résultats et les interprétations.
Taille d’un échantillon, une illustration opérationnelle
Vous souhaitez mener une enquête téléphonique. Pour des raisons de coûts, vous ne souhaitez pas solliciter vos 1000 clients. Le graphique ci-dessous vous permet de définir la taille de votre échantillon optimale en fonction de la marge d’erreur et du niveau de confiance que vous estimez acceptable. Plus vos exigences de précision sont élevées, plus l’échantillon devra être grand.
Ainsi pour obtenir un résultat à un niveau de confiance de 95% et une marge d’erreur de 2%, il sera nécessaire de valider 706 enquêtes.
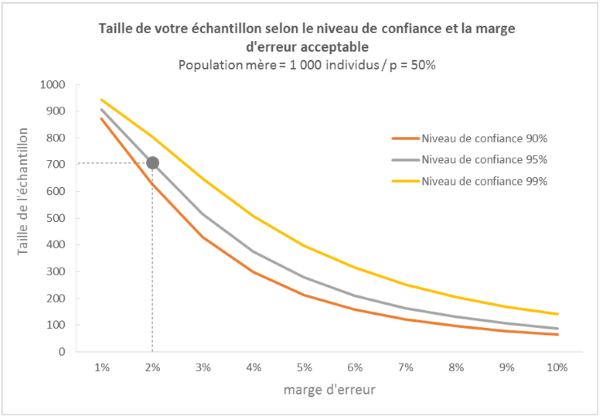
Plus la taille de l’échantillon est grande, plus la mesure est précise.
[1] Il existe différentes méthodes d’échantillonnage, chacune avec leurs avantages et leurs inconvénients.
[2] Pour redresser un échantillon, on attribue un poids à chaque répondant selon la strate à laquelle il appartient. Si l’on compte 50% des répondants appartenant à la strate A alors qu’elle représente 70% dans la population mère, on attribuera le poids de 70%/50% à chaque répondant de la strate A.
[3] La formule [3] s’écrit :
![]()
avec f = mesure du phénomène
n = taille de l’échantillon